A derivative is a kind of calculus that is used widely to differentiate functions according to their variables. Calculus is a branch of mathematics frequently used to solve complex problems or find changes in functions.
This branch of mathematics allows us to solve problems mathematically because, before calculus, all problems were solved statistically. Derivatives, integrals, limits, and power series are the main branches of calculus.
In this article, we’ll learn about the definition of the derivative, its working, and how to solve the problems of derivatives by using the chain rule.
Definition of derivative
Table of Contents
According to Bright Storm, the definition of the derivative is:
In calculus, the slope of a line tangent to the curve at a specific point. In other words, the instantaneous rate of change of the limits of the functions as time approaches zero among the measurements is said to be the derivative of the function.
The derivative can be calculated for many types of functions, such as constant, linear, power, exponential, polynomial, or logarithmic functions. It calculates the derivatives of these functions with respect to their independent variables, so it is also known as a differential.
The notation used to differentiate the function is d/dx, where x can be changed with any independent variable. The limits in calculus are widely used to define the differentiation of functions.
d/dx g(x) = limh→0 (g (x + h) – g(x)) / h
- d/dx is a differential notation.
- Lime is the limit notation.
- h is a specific point.
- g(x) is the given function.
Rules of differentiation
There are various rules of differentiation used to differentiate the function corresponding to the independent variables.
- Sum rule: d/dx [g(x) + h(x)] = d/dx g(x) + d/dx h(x)
- Difference rule: d/dx [g(x) – h(x)] = d/dx g(x) – d/dx h(x)
- Constant rule: d/dx [A] = 0, where A is any constant
- Constant function rule: d/dx [Af(x)] = Ad/dx [f(x)], where A is any constant
- Power rule: d/dx [f(x)] n = n[f(x)] n-1
- Product rule: d/dx [g(x) * h(x)] = h(x) * [d/dx g(x)] + g(x) * [d/dx h(x)]
- Quotient rule: d/dx [g(x) / h(x)] = 1/(h(x))2 [h(x) * [d/dx g(x)] – g(x) * [d/dx h(x)]]
- Chain rule: dy/dx= [dy/du * du/dx]
How to calculate derivatives by using the chain rule?
The problems of derivatives can be solved easily by using the rules of differentiation. The following are a few examples of derivatives solved by using the chain rule. Keep one thing in mind: to apply the chain rule, you also need to use the other rules of differentiation.
Example 1
Find the derivative of 3x3 + 4x2 + sin(x) + 34 with respect to x.
Solution
Step 1: Use the differential notation to write the given function.
d/dx [3x3 + 4x2 + sin(x) + 34]
Step 2: Apply the sum rule of differentiation and write the derivative notation with each function separately.
d/dx [3x3 + 4x2 + sin(x) + 34] = d/dx [3x3] + d/dx [4x2] + d/dx [sin(x)] + d/dx [34]
Step 3: Apply the constant and the constant function rule.
d/dx [3x3 + 4x2 + sin(x) + 34] = 3d/dx [x3] + 4d/dx [x2] + d/dx [sin(x)] + 0
= 3d/dx [x3] + 4d/dx [x2] + d/dx [sin(x)]
Step 4: Now use the power rule of differentiation d/dx [f(x)] n = n[f(x)] n-1 where n = 2, 3.
d/dx [3x3 + 4x2 + sin(x) + 34] = 3 [3x3-1] + 4 [2x2-1] + d/dx [sin(x)]
= (3 * 3) x3-1 + (4 * 2) x2-1 + d/dx [sin(x)]
= 9x2 + 8x1 + d/dx [sin(x)]
= 9x2 + 8x + d/dx [sin(x)]
Step 5: Use the chain rule to find the differential of sin(x).
d/dx sin(x) = d/du sin(u) * du/dx, where u = x
d/dx [3x3 + 4x2 + sin(x) + 34] = 9x2 + 8x + cos(x) d/dx [x]
= 9x2 + 8x + cos(x) [1]
= 9x2 + 8x + cos(x)
= x (9x + 8) + cos(x)
You can also get the step-by-step solution to differential calculus problems to avoid lengthy calculations by using a derivative calculator. Follow the steps below to use this calculator.
Step 1: Input the function.
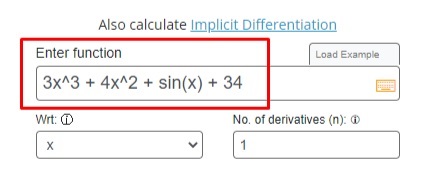
Step 2: Select the corresponding variable.
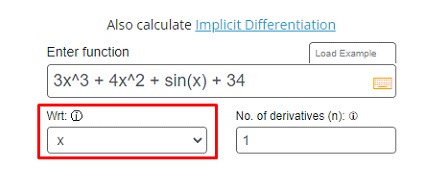
Step 3: Write the order of derivative e.g., 1 for the first derivative.
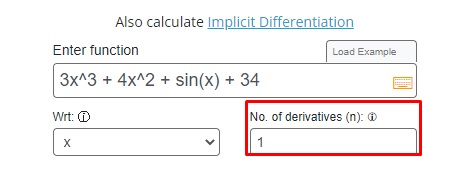
Step 4: Hit the calculate button.

Step 5: The step-by-step solution of the given function will show below the calculate button in a couple of seconds.
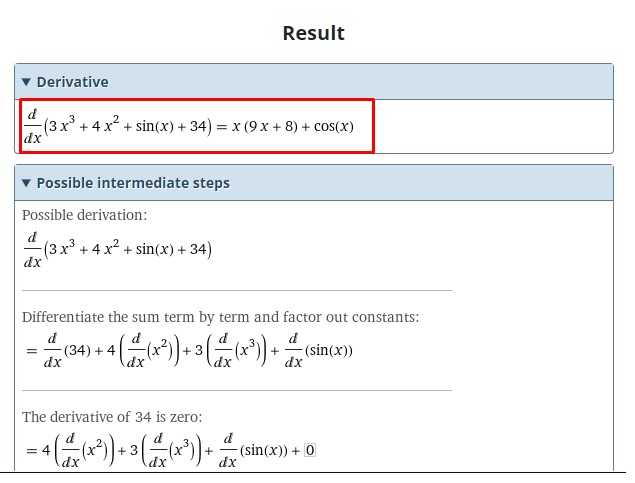
Example 2
Find the derivative of 13x2 – 14x – 4cos(x) – 54 with respect to x.
Solution
Step 1: Use the differential notation to write the given function.
d/dx [13x2 – 14x – 4cos(x) – 54]
Step 2: Apply the difference rule of differentiation and write the derivative notation with each function separately.
d/dx [13x2 – 14x – 4cos(x) – 54] = d/dx [13x2] – d/dx [14x] – d/dx [cos(x)] – d/dx [54]
Step 3: Apply the constant and the constant function rule.
d/dx [13x2 – 14x – 4cos(x) – 54] = 13d/dx [x2] – 14d/dx [x] – 4d/dx [cos(x)] – 0
= 13d/dx [x2] – 14d/dx [x] – 4d/dx [cos(x)]
Step 4: Now use the power rule of differentiation d/dx [f(x)] n = n[f(x)] n-1 where n = 1, 2.
d/dx [13x2 – 14x – 4cos(x) – 54] = 13 [2x2-1] – 14 [1x1-1] – 4d/dx [cos(x)]
= (13 * 2) [x2-1] – (14 * 1) [x1-1] – 4d/dx [cos(x)]
= 26 x1 – 14 x0 – 4d/dx [cos(x)]
= 26x – 14(1) – 4d/dx [cos(x)]
= 26x – 14 – 4d/dx [cos(x)]
Step 5: Use the chain rule to find the differential of cos(x).
d/dx cos(x) = d(cos(u))/du * du/dx, where u = x
d/dx [13x2 – 14x – 4cos(x) – 54] = 26x – 14 – 4(-sin(x)) [d(x)/dx]
= 26x – 14 + 4sin(x) [1]
= 26x – 14 + 4sin(x)
= 26x + 4sin(x) – 14
Summary
In this article, we’ve learned about the definition, working, and rules of differentiation along with examples. Now you can solve any problem of differential equations just by learning the basics of this post.


