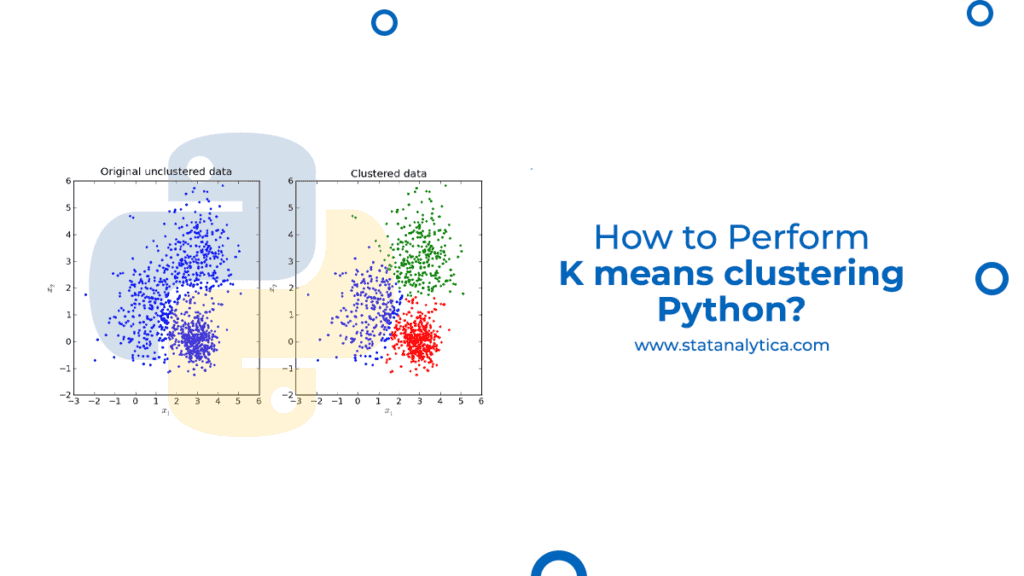
The k means clustering Python is one of the unsurprised machine learning methods applied to identify data object clusters within a dataset. There are various kinds of clustering methods, but it has been seen that k means is the oldest and most preferred clustering method. Because of this, k-means clustering in Python is the straightforward method that various data scientists and programmers adopt. If you want to know how to implement k-means clustering Python, then keep scrolling the blog. In this blog, we have covered all the necessary details about the K-means clustering, and an example is also detailed to help you the clustering’s functioning.
What are clustering and its application?
Table of Contents
Clustering is defined as the set of methods used to separate or partitioning data into clusters and groups. Clusters are the data object groups that are similar to another object within the cluster (as that of other cluster’s data objects). Practically, cluster supports to identify the two different data qualities:

- Meaningfulness
- Usefulness
| Meaningfulness Clusters | Usefulness Clusters |
| It expands the domain of knowledge. | It serves to be an intermediate step for pipelining the data. |
| For example, various researchers used the clustering method in the medical field to do gene expression experiments. This method results in identifying patients who respond oppositely to the particular medical treatment. | For example, several businesses use the concept of clustering for client segmentation. In which the clusters comprise the customer who does similar purchasing by which businesses can easily create targeted advertising campaigns. |
Apart from these, several other applications of k means clustering Python, like social network analysis and document clustering. Therefore, it can be concluded that these applications are appropriate almost in each industry. That is why clustering becomes a valuable skill for the experts who are working with different data.
What are the different clustering techniques?
Choosing the relevant clustering algorithms for the specific dataset is always challenging as there are various choices available for it. There are some of the essential parameters that always affect the decision, such as the dataset features, cluster characteristics, number of data objects, and the number of outliers. Below, we have mentioned the 3 most renowned categories of clustering algorithms:
- Partitional clustering
- Density-based clustering
- Hierarchical clustering

Partitional Clustering
It separates the data objects from the non overlapping group. Or we can say that no object could be the member of multiple clusters, and each cluster has at least a single object.
In this technique, the user must declare the number of clusters, which are indicated with the variable k. Several partitional clustering algorithms always work as an iterative process to specify the particular data object dataset into the k cluster. K-medoids and k-means are examples of partitional clustering algorithms.
Density-based Clustering
It analyzes cluster assignments depending on the data point density in a particular region. Cluster is assigned in the region where low-density regions classify high-density data points.
Just as that of other clustering categories, it does not need to declare clusters’ numbers. But, distance-based factors always act to be a tunable threshold (the threshold can analyze how close the points can be considered to a clustering member). OPTICS (Ordering Points To Identify the Clustering Structure) and Noise are some of the examples of density-based cluster algorithms.
Hierarchical Clustering
It also analyzes the clustering assignments by creating a specified hierarchy. It can use two different approaches, and that is:
| Divisive clustering: The top-down approach always starts with the points as a single cluster and divides the less similar cluster at the specific step until the single data point does not remain. |
| Agglomerative clustering: The bottom-up approach always merges the two similar points until the points do not merge as a single cluster. |
This technique produces the tree-like hierarchy of different points, and these are known as a dendrogram. As that of partitional clustering, the cluster numbers (k) is always predestined by the user.
Which is the most useful method for k means clustering Python?
UNDERSTAND THE K-MEANS ALGORITHM
It has been observed that a conventional k means need just a few steps to execute. That starts with selecting k centroids, where the value of k = the number of clusters that you have selected. Centroids are the specialized data points that represent the cluster’s center.
The k means clustering Python algorithm’s main components always work in a two-step process known as expectation-maximization. Initially, the expectation step is assigned by every data point to a specific centroid that is nearer to it. Then, with the help of the maximization step, the computation of the nearer points can be done. This algorithm works as:
| Specifying the number of k clusters to assign the value.Initializing the k centroid randomly.Repeat the process.Expectation: Assigning every point to its nearer centroid.Maximization: Computing the mean (or new centroid) of every cluster.Till the position of the centroid does not change. |
The cluster assignments’ quality can be determined by computing the SSE (Squared Error) after matching the previous iteration’s assignment or using centroid converge. SSE measures the error that is trying to minimize the k means value. The below-mentioned figure can display SSE and centroids that update the first five iterations in the different runs.
In this figure, you can check the initialization of the particular centroid. Moreover, it highlights the objective of SSE that use to measure clustering performance. Once the several clusters are chosen and initialized the centroids, the expectation-maximization step will repeat till the position of the centroid converges and unchanged.
An example of k means clustering Python
Create the DataFrame for the 2D dataset
To start with the example, let’s take an example of the following 2D dataset:
| x | y |
| 22 | 78 |
| 35 | 51 |
| 20 | 52 |
| 25 | 76 |
| 32 | 57 |
| 31 | 72 |
| 20 | 71 |
| 34 | 55 |
| 32 | 67 |
| 65 | 73 |
| 52 | 49 |
| 55 | 30 |
| 42 | 38 |
| 50 | 45 |
| 55 | 51 |
| 57 | 34 |
| 50 | 33 |
| 63 | 56 |
| 45 | 57 |
| 47 | 48 |
| 46 | 23 |
| 33 | 18 |
| 31 | 12 |
| 43 | 10 |
| 45 | 18 |
| 36 | 3 |
| 41 | 27 |
| 51 | 6 |
| 44 | 5 |
You can write the data for k means clustering Python with the help of Pandas DataFrame.
| from pandas import DataFrame Data = {‘x’: [22,35,20,25,32,31,20,34,32,65,52,55,42,50,55,57,50,63,45,47,46,33,31,43,45,36,41,51,44], ‘y’: [78,51,52,76,57,72,71,55,67,73,49,30,38,45,51,34,33,56,57,48,23,18,12,10,18,3,27,6,5] } df = DataFrame(Data,columns=[‘x’,’y’])print (df) |
Output:
| x | y | |
| 0 | 22 | 78 |
| 1 | 35 | 51 |
| 2 | 20 | 52 |
| 3 | 25 | 76 |
| 4 | 32 | 57 |
| 5 | 31 | 72 |
| 6 | 20 | 71 |
| 7 | 34 | 55 |
| 8 | 32 | 67 |
| 9 | 65 | 73 |
| 10 | 52 | 49 |
| 11 | 55 | 30 |
| 12 | 42 | 38 |
| 13 | 50 | 45 |
| 14 | 55 | 51 |
| 15 | 57 | 34 |
| 16 | 50 | 33 |
| 17 | 63 | 56 |
| 18 | 45 | 57 |
| 19 | 47 | 48 |
| 20 | 46 | 23 |
| 21 | 33 | 18 |
| 22 | 31 | 12 |
| 23 | 43 | 10 |
| 24 | 45 | 18 |
| 25 | 36 | 3 |
| 26 | 41 | 27 |
| 27 | 51 | 6 |
| 28 | 44 | 5 |
K means clustering Python (3 clusters)
Once you are done with creating the DataFrame depend on the above set of data, you are required to import some of the additional Python modules:
- matplotlib – to create charts in the Python
- sklearn – to apply the k means Clustering Python
The below-mentioned code is used to declare the number of clusters. To understand it, let’s take an example of 3 clusters:
KMeans(n_clusters=3).fit(df)
| from pandas, let’s import the DataFrameimport matplotlib.pyplot as pltfrom sklearn.cluster import KMeans Data = {‘x’: [22,35,20,25,32,31,20,34,32,65,52,55,42,50,55,57,50,63,45,47,46,33,31,43,45,36,41,51,44], ‘y’: [78,51,52,76,57,72,71,55,67,73,49,30,38,45,51,34,33,56,57,48,23,18,12,10,18,3,27,6,5] } df = DataFrame(Data,columns=[‘x’,’y’]) kmeans = KMeans(n_clusters=3).fit(df)centroids = kmeans.cluster_centers_print(centroids) plt.scatter(df[‘x’], df[‘y’], c= kmeans.labels_.astype(float), s=30, alpha=0.6)plt.scatter(centroids[:, 0], centroids[:, 1], c=’red’, s=30)plt.show() |
Run the above code, and you can check the 3 clusters at 3 different centroids:
Notice that each cluster’s center (in the red color) describes the observations’ mean, which belongs to a particular cluster. Additionally, you can analyze that the observations are much closer to the cluster’s center than that of the other clusters’ centers.
Conclusion
K means clustering Python is one of the concepts that fall in the category of unsupervised machine learning methods. Moreover, its algorithm is used for finding groups in unlabeled data. This blog has mentioned the details about clustering techniques and created the DataFrame for the 2D dataset. Additionally, we have explained an example to find the centroid of 3 clusters. If you find any issue with the concept of clustering, you can contact us and ask your query to our experts by commenting in the comment section. We will provide you with a quality solution related to your query. So, keep learning and keep practicing. we provide you the best python programming help at a low cost.