Nowadays, you all have watched the news about coronavirus vaccination. And there are so many people who might be thinking about how an agency or medical organization says that this particular vaccine is useful to treat this virus. Well, this is because of the Standard deviation value. Moreover, this is the correct place where the importance of standard deviation is being judged.
How?
Let me clear this point to you.
During the testing of antiviral medicine, the number of samples of a virus is tested using the particular antiviral vaccine. The experiment is also monitored over a specific time duration.
The standard deviation comes into the role as it uses to calculate the mean of the virus elimination rate. The value of the SD is helpful to prove that the particular antiviral has a similar effect on the sample populations.
Now, we can see that SD can play an important role in testing antibiotics. Apart from this, there are several uses of SD. Below, check the importance of standard deviation with a useful example.
What Is The Standard Deviation?
Table of Contents
It uses for measuring the response time that is spread around the Mean. Or in simple words, we can understand it as the smaller the value of SD, the more logical or consistent the response time.
Formula to calculate Standard deviation:

| Key point: You can not effectively link two datasets without using the standard deviation. Let’s understand it with an example. If the average of two data sets is equal, it does not imply that the datasets are also similar. Suppose you have a dataset as 200, 199, 201 and others like 200, 0, 400. Both have the same average which is 200. But have different SD the first has SD =1 and the second has SD =200. Therefore, we can say that without SD, it is not easy to check whether the datasets are closer to the mean value or the data is spread over a large range. |
History of Standard Deviation?
Karl Pearson introduced the concept of Standard Deviation in the year of 1893. Standard Deviation is the widely used and most important measure of dispersion.
Many people might get confused regarding whether Root Mean Square Error (RMSE) is the same as Standard Deviation. So, let us clear this up for you.
They are not the same. Standard Deviation is used to measure the spread of data around the mean, while Root Mean Square Error is used to measure the distance between some values and the prediction for those values.
Why Is Standard Deviation Useful?
Here are some reasons why standard deviation is useful:
1. Helps To Calculate Information From Data
Standard deviation helps us understand how spread out the data points are from the average. A higher standard deviation indicates greater variability, while a lower value shows data points are closer to the mean.
2. Risk Assessment
In finance and investments, the standard deviation is used to assess the risk associated with an investment. A higher standard deviation implies higher uncertainty and risk, which may be undesirable for conservative investors.
3. Comparing Distributions
When comparing two or more data sets, standard deviation allows us to see which dataset has more variability, helping to identify trends or differences.
4. Confidence Intervals
Standard deviation is used in calculating confidence intervals, which provide a range of values where the true population parameter is likely to lie. It helps researchers express the uncertainty in their estimates.
5. Quality Control
Standard deviation monitors consistency in manufacturing and quality control processes and detects product performance or measurement variations.
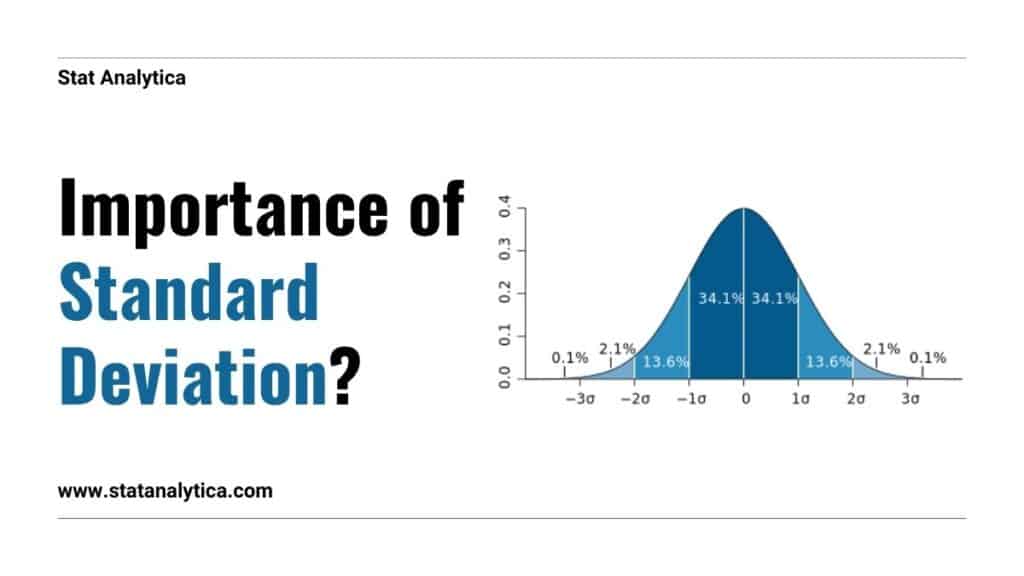
6. Normal Distribution
Standard deviation plays a crucial role in the normal distribution, where about 68% of data falls within one standard deviation from the mean and about 95% within two standard deviations.
7. Statistical Analysis
Standard deviation is fundamental in various statistical analyses, such as hypothesis testing and regression analysis, helping researchers draw meaningful conclusions from data.
Is There Any Disadvantage Of Using Standard Deviation?
Yes, there is!!! But not as much as you might be thinking.
- Like, it might look hard to calculate for some people.
- It assumes the pattern of normal distribution.
- It is unable to provide the full range of data.
- SD uses only the data statistic, which plots independent variables against the frequency.
| Note: |
| What do you mean by volatility? In trading, volatility measures the correlation between performance variance and the reference market. In a nutshell, volatility shows us how an asset (such as stock) performs compared to a market. One of the techniques for determining the volatility of financial activity is the Standard Deviation. |
Is There Any Technical Viewpoint Of Standard Deviation?
For those traders who enjoy mathematical studies, we will look at the Standard Deviation from a technical perspective. “Root-mean-square deviation” is another term for the Standard Deviation. It is an estimate of the volatility of a random variable and represents an index of dispersion of experimental observations (such as the market price).
The dispersion around an expected result or estimate is taken into account when computing the Standard Deviation. Standard deviation is also known as “precision” in the world of statistics.
What Is The Standard Error?
The SE or Standard Error of a statistic is the Standard Deviation of its sampling distribution or an estimate of that standard Deviation. On the other hand, if the statistics are the sample mean, it is called the SEM ( Standard Error of the Mean ).
However, the Standard Error, or SE, is very similar to the Standard Deviation. Whereas, the standard error uses statistics which is sample data and standard Deviation uses parameters which is population data.
Tip:
If you are doing research, do not collect data on a small sample of the whole population. Because you’re likely to end up with different sets of values with different means each time.
When you take enough samples from the population, the means will be arranged into a distribution around the true population mean.
As a result, the standard deviation of the sample means is called the Standard Error.
How to calculate standard error?
You can calculate standard error with this formula that is given below, where σ (this sign) represents the standard Deviation and n represents the sample size.
SE = standard error of the sample
σ = sample standard Deviation
n = number of samples

The standard error increases when the variance of the population increases, i.e. standard Deviation.
Standard error decreases when the size of the sample increases – as the sample size gets closer to the real size of the population, the sample means cluster more and more around the true population mean.
That’s how you calculate the standard error. If you are still confused?
Don’t worry; below is an example of a Standard error.
Example of Standard Error:
To get a better understanding of the standard formula error, here’s an example:
Imagine we have a population of 80 people, and we are interested in their height. We measure their height and then calculate the standard Deviation as 30.6 cm. We now need to put these values into our equation:

If you are not comfortable putting equations into calculators, you can break down the formula into manageable pieces. Below are some steps that you can take.
Firstly, calculate the square root of the number of samples that is (n). In this case, n is 80. The square root of 80 is 8.94.
Next, divide the standard Deviation that is (30.6) by the square root of 80, which is (8.94). By doing this, we get the value of 3.42.
As a result, the standard error is 3.42 cm in our population for height.
Let’s Check The Real-Life Example Of The Importance Of Standard Deviation
Here in this section we will tell you some of the best real life example on the importance of standard deviation:
1. Distribution of salary
Assume that Business A’s average wage is $80,000, with a standard deviation of $20,000. Because of the significant standard deviation, there is no assurance that you will be paid close to $80,000 per year if you work at the organization because salaries vary so much.
In contrast, imagine business B’s mean compensation is $80,000, but the standard deviation is only $4,000. Because the standard deviation is so little, you may be confident that you’ll get paid close to $80,000 because wages vary so little.
If we made a boxplot to represent the salary distribution at these two firms, it would look like this:
Because the standard deviation of wages is thus much higher, the length of the boxplot for firm A is comparatively higher.
Although both firms have the same mean salary, company A has a significantly wider compensation range.
2. Distribution of House Prices
Assume the median property price in neighbourhood A is $250,000, with a $50,000 standard deviation. Because the standard deviation is so high, some of the housing values will be much higher than $250,000, while others will be much lower. There’s no assurance that if you look at a property in this neighbourhood, the price will be near to the mean.
On the other hand, assume that the mean property price in neighbourhood B is similarly $250,000, but the standard deviation is just $10,000. Because the standard deviation is so low, you can be confident that any property you see in the neighbourhood will be near to this price.
It may look like this if we made a boxplot to depict the distribution of property values in these two neighbourhoods:
Because the standard deviation of property values is so much higher in neighbourhood A, the length of the boxplot is significantly longer.
In reality, housing prices in area A range from less than $150k to more than $400k. At the same time, prices in neighbourhood B are only around $230k to $270k.
We can estimate how much price variation to expect in each community just by knowing the standard deviation of property prices in that neighbourhood.
3. In stock market
When deciding whether or not to invest in a stock, the standard deviation can be used to assess risk. A stock with an average price of $50 and a standard deviation of $10 is expected to trade between $30 ($50-$10-$10) and $70 ($50+$10+$10). And it is 95% of the time (two standard deviations). It’s fair to predict that it will drop or skyrocket outside of this range 5% of the time.
If you compare this to a stock with an average price of $50 but a standard deviation of $1, you can expect the stock to close between $48 and $52. And it is almost 95% certain. The second stock is safer and more reliable. The risk increases as the standard deviation grow in comparison to the mean. For example, blue-chip stocks would have a low standard deviation with respect to the mean.
Check the importance of Standard Deviation for performance testing.
Before moving to understand the importance of SD in various fields, let’s check how to check performance using SD. The SD tells if the response time of the variables is constant throughout the testing or not.
If the value of the SD is smaller, then the more constant the transaction response time is. This shows that you are delivering an excellent experience to your end-users.
Let’s check an example of it to get a clear picture of it.

In this example:
- The mean of the transaction variables is similar. Therefore, you are unable to test the result on the basis of the mean. That is why average is useless in this case.
- The 90% of “search” is much better as compared to others. Therefore, it considers being an important metric to calculate response time.
- It is quite clear that the “logout” transaction has the lowest SD. This implies that the response time is more constant than the others.
Finally, we get the best performer that is logout, but here we require to check the two requests for another request for the tuning purpose.
How To Calculate The Standard Deviation?
There are various tools by which you can easily check the SD of the variables. But if you want to get familiar with the magic of SD calculation, then follow the below steps.
| Calculate the average of the sample numbers. |
| Subtract average from every number and take the square of the value. |
| Sum all the values and divide them with (N-1). |
| Calculate the square root of all. Finally, you got the standard deviation. |
Now, check the search transaction response time.
| Average = (2 + 3 + 1 + 15 + 4)/5 = 5. |
| (2-5)^2 = (-3)^2 = 9;(3-5)^2 = (-2)^2 = 4;(1-5)2 = (-4)^2 =16;(15-5)^2 = (10)^2 =100;(4-5)2 = (-1)^2 = 1; |
| (9 + 4 + 16 + 100 + 1)/4 = 32.5 |
| √32.5 => 5.7 |
Additional Point: What Is The Importance Of Standard Deviation In Various Fields?
Here in this section we will tell you some additional points on the importance of standard deviation in various fields:
1. In Finance
The standard deviation is used in finance by business owners to understand risk management and make better business decisions. It helps in calculating the margins of error that occur in the survey reports taken by an organization or company.
Let’s take an example of it.
| Suppose you have a logistics and transportation business. You can now use standard deviation to know how many drivers you need to run the business. Moreover, the SD is also useful to calculate risk-adjusted returns using the Sharpe ratio. This helps in getting the reasons to get the maximum results by considering the minimum risk. |
2. Quality Control
Quality control in manufacturing and production is important to keep the standards. It is used to test the output sample against a particular standard.
If the SD is greater than expected, then the samples are rejected because they do not match with the standard sets. There are several soft drink companies that use it to check the sugar content in the product using standard deviation.
Let’s understand it through an example:
| Suppose a coke can have a mean of 250ml and ±2ml is SD; it means the minimum coke capacity is 252ml and 248ml. It means lesser and greater than this value is distributed by the company. |
3. Polling
Polls use to know who is going to win the election. The standard deviation can help in calculating the margin of error. Those are useful in calculating the poll result.
Example:
| Suppose you ask different groups (100 people groups) about who they will vote for. Here you can use the samples’ answers for calculating the margin of error and the difference. Moreover, it tells you the reliability of the polls. |
4. In Business
It is known to all that a company and employee always have some conflict among them. These conflicts relate to salary packages and are unfair to some employees.
The employee can check the difference in their salary with the average salary and standard deviation of the other company employees. If the SD is higher than expected, then the owner must look into the matter.
Let’s understand it with an example:
| If you go through the accounts and you realize that your senior’s salary data has a higher SD, then it is time to check the reason. Once you check the reason, you found that your senior gets the higher salary because of the experience of 10 years. Then it is fair that the company pays the higher salary to the senior. |
5. In daily life:
Most people do not have any idea that they use Standard deviation in their daily life. There are numerous examples that show that we use SD concepts even without knowing.
Some of the examples are:
| Weather forecasters use SD to predict the weather of the cities, country, or even the world. Teachers use the concept of average and SD to calculate the result of the test. In budgeting, everyone uses the SD to check how much money they should spend. Or they might be spending much more money than expected. |
A Quick Recap About Standard Deviation
The Standard Deviation of a data set reflects the degree of variation in the data set by measuring and averaging how far each value in the data set differs from the computed mean. The standard deviation formula differs depending on whether you’re analysing population data (in which case it’s called ) or predicting population standard deviation from sample data (in which case it’s called s).
Conclusion
Quality testing and factors are some of the important things that a company needs to take care of. This can be calculated using the standard deviation. Above, I have mentioned all the importance of standard deviation in various fields.
Once you understand where the SD concept is applicable, you can easily use it. If you are unable to understand anything about SD, then comment in the below section. If you want someone to do my statistics homework for me. Then, I will always help you solve your query related to statistics concepts in the easiest way.
“Keep on learning and practicing the concepts of statistics with our quality blog.”
Frequently Asked Questions
What is the use of standard deviation in real life?
You can easily use standard deviation to match two or more sets of data. For instance, a weather forecasting reporter analyzes the high temperature that uses to forecast the two different weather patterns of cities. The lower SD value would define a reliable weather prediction.
What are the uses of standard deviation in statistics?
SD is used for measuring the range of data distribution. Moreover, it calculates the distance between every data point and the average. The formula for SD depends on whether the collected data is estimated as a sample population of its own or the sample expressing the value of a larger population.
What are the special advantages of standard deviation?
The advantage of SD are:
It provides a more realistic view of how the data is shared.
Determines how much data is gathered throughout an average value.
SD does not affect extreme values.