Have you ever imagined which mathematical branch is mostly used? Well, the straightforward answer to this question is statistics and calculus. So, do I need to learn statistics vs calculus?
Yes, you should!! The reason is that both have several real-life applications. Calculus concepts present from your cell phone, car, and TV to the economy, national defence, and medicine. Moreover, statistics concepts are also useful for analysis, observation, and mathematical predicting models.
Find this quite useful? Yes!! Below I have mentioned the necessary information regarding statistics vs calculus. Before that, let’s take an overview of what statistics and calculus are.
On the other hand, if you are looking for a statistics homework helper, then don’t worry you can get the best statistics homework help from our experts. So, what are you waiting for get help now!
An overview: Statistics vs Calculus
Table of Contents
What are statistics?
Statistics is a form of Statistical analysis of something. It can be related to anything like any business. That is why we say that statistics is a form of statistical analysis of anything.
We can check the growth of something, or we can track the growth or maybe the downfall of any business with the help of statistics or with the help of statistical analysis we will be doing with it.
What is calculus?
Calculus, the first thing you should know about that is calculus is also called infinitesimal calculus. Or the calculus of Infinitesimal.
And it is used for the study of continuous changes that may happen in any mathematical situation like geometry is the study of shape, the same that calculus is the study of continuous changes.
Statistics vs calculus: Trending graph
From the graph, it is clear that statistics are in greater demand. As a result, Calculus lags and doesn’t give head-to-head competition.
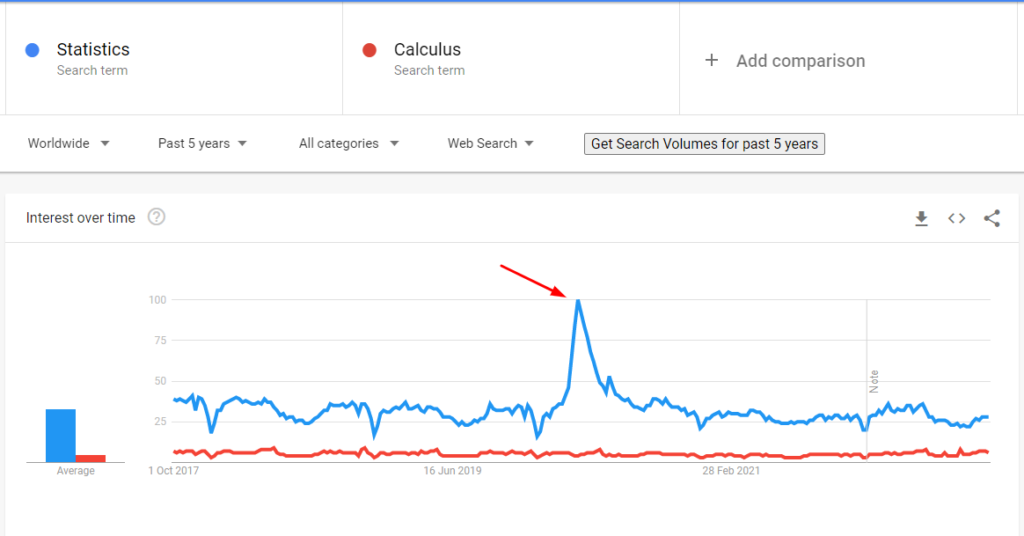
Apart from this, there is a high peak in demand for statistics in April 2020. After that, there is a drop in its demand. At the same time, calculus has a continuous graph with almost constant demand.
On the other hand, this doesn’t mean that statistics are better than calculus. Both have their advantages and disadvantages at the same time, and it totally depends on the user’s needs.
Statistics vs Calculus
Let’s take Calculus and discuss it
Analytics is “legitimate” arithmetic. It is exquisite and flawless, and you find the right solutions. You don’t need to compose sentences. Ever! The majority of the issues are quite hypothetical, so you don’t need to manage “word issues.”
The educators like Calculus and battle about who gets the chance to instruct it. They feel certain about what they are doing. They have shown it for quite a long time and don’t have to do anything new. There are seas of online recordings, games, and assets to support understudies. Khan institute recordings are valuable.
Yet, you don’t have to approach the PC space to do analytics. Guardians are bound to know analytics (however very much overlooked) than insights.
Analytics is required for significant subjects, for example, building, material science, and… Hmm, can’t think of anything else! Goodness, yes – more math. It is a decent mental order that assists with critical thinking abilities.
It may very well be really fun if everyone is instructed. Other than individuals, revealing insights is the simple alternative for individuals who can’t do analytics.
Not it’s time for us to take Statistics and Discuss it
So, as we all know, Estimates relate to life, it is confusing, and normally the suitable reactions aren’t clear, so understanding and acceptance are critical. You ought to form reports and impart them on paper. This will help you with working up your fundamental thinking aptitudes and social capacities.
You have to understand significant material, for instance, science, money-related issues, or games.
New Zealand is driving the world by introducing resampling, randomization, bootstrapping, and time plan assessment at an optional school level. The online resources are very few. Anyway, those enduring (and in our pipeline) are focused on your use.
Watchmen are unpracticed with estimations, yet you will find what you are doing fascinating. You get the chance to do an enormous part of your relies on the PC, comparably as authentic examiners do.
You will never wind up asking, “For what reason do we need to get comfortable with this?” since it is clear how it is a bit of your life. You will be better prepared to see the truth from lies on the web. You will end up looking at the world in a sudden manner.
Bits of knowledge is required for certain subjects: cerebrum science, science, planning, the board, advancing, medicine, humanism, guidance, geology, topography, law, and news inclusion. It furthermore broadens the expected results in the examination of articulation subjects, for instance, History and English.
Statistics vs Calculus: Tabular form
| Statistics | Calculus |
| Deal with the methods and process of collecting the data and analyzing it. | Deal with numerical, graphical, and algebraic data to solve difficult problems. |
| Statistics concepts are based on computation de-emphasized. | The concepts are based on pre-calculus. |
| It concentrates on the interpretation and communication of the information. | It focuses on the computational proficiencies of the problems. |
| The conclusions are made quite critical. | The approach used in calculus emphasizes techniques. |
| Crucial for Arts, Business, and Data-intensive areas. | Crucial for business and STEM (Science, Technology, Engineering, Maths). |
| Skills required for statistics are reading and analyzing skills, effective calculation, and high thinking abilities. | The skills required for calculus are understanding of previous math and logical thinking abilities. |
Also Read
- Statistics Vs Parameter: All You Need to Know
- Why Study Statistics | What Are The Top Most Reasons to Study Statistics?
- Top Most Important Application of Statistics in Daily Life
Should I take statistics or calculus first?
Statistics help in improving advanced-level thinking. Moreover, it is present in all aspects of life and helps in understanding calculus problems effectively. Therefore, it is always better to take statistics first.
But in case you find statistics a bit difficult, then go with calculus.
Now the question arises here: Is calculus or statistics easier?
Well, it depends on person to person. Some students find statistics difficult, and others find calculus a bit difficult.
That is why it can vary from person to person. But if you practice regularly, then you can easily develop and enhance your skills. So, practice regularly.
Statistics vs Calculus Which Is Harder

If you take an introductory statistics course, you will encounter some simple concepts to work out and solve.
However, as statistics progresses further, the overall process becomes significantly more difficult.
On the other hand, calculus is commonly considered the most difficult math subject due to its abstract nature. Even though most people explore calculus and see what it takes to understand the solutions to problems. Calculus is a much narrower branch of mathematics than statistics.
Another thing to consider is that in order to do calculus, you will need to have a general understanding of statistics.
Statistics is another branch of mathematics that you will use throughout your life. Even simple statistics can help us plan out our lives. Calculus does not always have the same uses as statistics.
As a result, Statistics is more difficult than calculus, especially at the advanced levels.
Conclusion (Statistics vs Calculus)
So, this was all about our topic for today, which was Statistics vs Calculus. We hope that you have learned from this, which we have discussed above, about our topic: Statistics vs Calculus.
And we hope that you have found it interesting; if so, then share this with your friends and colleagues so that they can also know about the differences and similarities between Statistics and Calculus.
Get the best calculus assignment help and calculus homework help from the experts. Also, if you are looking for someone who can do my statistics homework for money, we are here to help you.
FAQs
In this section I have mentioned four FAQs related to Statistics vs Calculus, which are as follows:
Q1. Do I need calculus to study statistics?
There are several calculus concepts present behind the statistical software working. These are helpful for estimating the factors that deal with modelling. If you know how this software works, you can understand the reason for using particular models.
Q2. Which is more important, calculus or statistics?
Calculus is quite beneficial for students who are pursuing majors in engineering or science. On the other hand, statistics are important for being an informed citizen. Also, it is useful for almost every major, career, and solving daily routine problems.
Q3. Which is better calculus or statistics?
Because statistics is a part of everyday life, it has more real-world applications than calculus. Calculus is more abstract and includes more visual concepts from geometry; thus, students who did not do well or enjoy geometry may not like calculus.
Q4. Is statistics or calculus easier?
Statistics is more difficult than calculus, especially at advanced levels. If you take an introductory statistics course, you will encounter very simple concepts that are simple to work out and solve.



Comments are closed.