If you do not have enough knowledge of statistics, then there is the chance that you feel like a trap by various statistics problems. T score vs z score is those two terms, which can confuse you.
But don’t worry, as I have explained all the necessary things related to t score and z score. Moreover, I have given a detailed head-to-head comparison of both t score vs z score. This will definitely help you clear your doubts related to the t score and z score. So, let’s begin with the details.
However, if you have pending maths assignment, then don’t worry you can get the best maths assignment help from mathematics experts.
What Is The T Score?
Table of Contents
T score considers the conversion of unstructured or raw data into the standard scores. It considers when the conversion depends on the sample standard deviation and sample mean.
If you do not have the population data set, you need to select sample data to carry out the sample SD and sample mean.
What Is The Z Score?
Z score considers as the conversion of unstructured or raw data into the standard scores. It considers when the conversion depends on the population standard deviation and sample mean.
It can be used in the case when you have the complete data set of the particular test.
Is there any specific formula to calculate the t score vs z score?
Yes, there is!
The T Score Can Calculate Using The Formula:
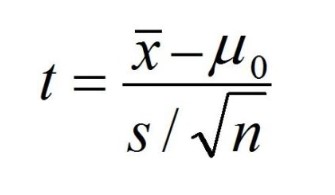
Where,
μ0 = population mean
x̄ = sample mean
n = sample size
s = sample standard deviation
If you do not have multiple items in the sample observation, the square root written in the denominator will become √1. It means the t-score formula will become:
Let’s Understand It Through An Example:
A university claims that the women who graduate from the university earn $300/hour on average. The sample of 15 graduates is taken as the $280 mean salary with an SD of $50. Find the t score of the university women’s graduate salary.
Solution:
Write each value in the above formula:
| => (280 – 300)/ (50/√15) => -20 / 12.9 => -1.549. |
The z score can calculate using the formula:
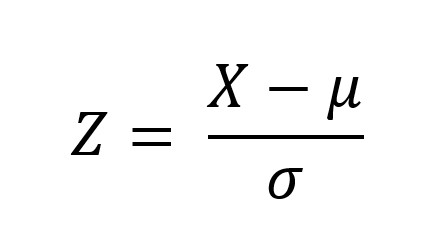
Where,
- μ = Population mean
- X = individual raw data
- σ = Population standard deviation
Let’s Understand It Through An Example:
Suppose you have the value of a test score of 180 with the mean of 140 and SD (standard deviation) of 20. Calculate the z score.
Solution:
| z = (x – μ) / σ |
| = (180 – 140) / 20 = 2. |
The z score indicates how many SDs the actual score is. In the above example, your z score is 2 SD above the mean. Now, let’s check the comparison of the t score vs z score.
Head To Head Comparison: T Score Vs Z Score
| Parameters | T score | Z score |
| Standardization of data | It is used for standardization from Sample SD and sample Data. | It is used for the standardization of population SD and population data. |
| Standard Deviation | The value of standard deviation in the t-score is always 10. | The value of standard deviation in z score is always 1. |
| Data Size | When the sample size value is less than 30, or the Population set is not known, it is better to use a T score. | When the Population set is above 30 or known, it is better to use a Z score. |
| Mean | A mean value is always 50. | A mean value is always zero. |
| Derived Result | The derived result of the t score is never negative. | Most of the time, the derived result of the z score can be negative. |
| Range | It ranges between the values of 20 and 80. | It ranges between -3 to 3. |
| Distribution | T score is a section of T distribution. | Z score is a section of Z distribution. |
| Preference | T score is preferable for the higher range values, but it has its inherent limitation with the increment in the size. | Z score is much less preferable, as it supports extensive data. |
| Use with the increase in size | Its application reduces with the increment in size. | The Z score can be used with the increment in size. |
Key Differences Between Z score vs T score You Should Know
Here are the 5 key differences between the Z score vs T score that you should know:
- Z-score is based on the standard normal distribution, while T-score is based on a t-distribution.
- Z-score has a standard deviation of 1 and a mean of 0. On the other hand, T-score has a mean of 50 and 10.
- The Z-score is commonly used in large sample sizes. However, T-score is used in smaller ones.
- Z-score compares individual data points to the population means, whereas T-score compares individual data points to a specific sample mean.
- Z-score is used in many statistical analyses, while T-score is mainly used in psychological and educational assessments.
Is There Any Specific Condition To Using T Score Or Z Score?
Yes, there is! Moreover, there is a rule to use them.
The t score can be used when the sample has:
- unknown population standard deviation,
- sample size less than 30.
Whereas the z score is used when you know:
- the population standard deviation,
- the sample size is larger than 30.
The above flow diagram is my own experience-based chart that you might have used in your elementary statistic classes. In real-life, it has been seen that the t-score is used with the t distribution.
Note: If the sample has more than 30 measurements, the normal distribution can use at the t distribution place.
Where Can You Use Z Score And T Score?
Once you understand the comparison of the t score vs z score, you can implement the use of both anywhere. Practically, the Z score is mostly used to check the possibilities of a company in the stock market that is going into bankruptcy. Moreover, the z-score in biostatistics is used for analyzing the human nutritional data, particularly for kids.
On the other hand, the t score is mostly used to check the fracture risk assessments, bone loss, bone mineral density, and normal bone density. Apart from this, the t-score is used where the statisticians do not know the population SD; and he/she has to make estimations using the sample.
| Things to remember: 1. T score and z score both describe SD from the average value. But when “0” of the z score has the value 0 SD from the mean, then “50” of the t score will give the same value as that of the z-score. 2. It is because the t score utilizes the average of 50, and the z score utilizes the average of 0. 3. When the t score is above 60, the score will be in the top 1/6th of the distribution value. When it is above 63, the distribution value will be the top 1/10th. 4. On the other hand, when the t score has below 40, it will describe the lowest 1/6th position. But if it is below 37, the distribution will be bottom 1/10th. |
Conclusion
When the conversion depends on the population standard deviation and population mean, then the user should prefer a z score. But when the conversion depends on the sample standard scores and sample mean, then the user should go with a t score.
Both have their own use and concepts. That is why the application and approach to use any of them can vary as per the statisticians’ needs. Above, I have explained all the necessary differences between the t score vs z score so that you can easily decide what you should use.
If you still have a query, don’t hesitate to ask me. Comment your queries in the below section, and I will try my best to help you with the query.
Also, get the best statistics assignment help from the statistics assignment help at a very reasonable price.
Frequently Asked Questions
Q1. What is a t score?
T score is the conversion of unstructured or raw data into the standard scores. It considers when the conversion depends on the sample standard deviation and sample mean.
If you do not have the population data set, you need to select sample data to carry out the sample SD and sample mean.
Q2. What do T scores and Z scores represent?
The z-score and t-score or you can call z-value and t-value show how many standard deviations away from the mean of the distribution you are, assuming your data follow a z-distribution or a t-distribution.
Q3. What is the difference between T-test and Z-test?
The key difference is that the Z-test is used when the population standard deviation is known, whereas the t-test is used when the population standard deviation is unknown and is estimated from the sample data.


